Optimistic probability estimates, or "How to unknowingly pick the wrong projects and mistakenly increase portfolio risk."
Managers and experts are often optimistic about their projects, overestimating each project's likelihood of success. How does this optimistic bias affect project selection? When I ask executives for their thoughts, sone say, "My biases are consistent over all of my projects, so the biases don't matter." This hypothesis is wishful thinking and it's wrong.
Figure 1 shows a decision tree with one chance node and two outcomes: success and failure. In this example, the probability of success is 50%; success produces a payoff of x and failure produces a loss of -x. The expected value of the tree is zero.
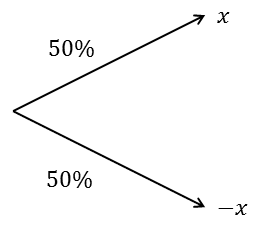
Figure 1: A decision tree with one chance node and a 50% chance of success. Success returns x and failure returns -x.
Using this decision tree, Table 1 shows how consistent optimistic biases affect project selection. The rows present different versions of the decision tree. The probability of success remains the same (50%), but the value of x varies. The expected value is the same for all of the examples but project risk increases with x.
For a risk adverse decision-maker, the table presents the examples in order of preference. The top row is the most attractive choice. It produces the same expected return as the other examples but with less risk. The bottom row is the least attractive choice, producing the same expected value as the other examples but with the greatest risk.
| Probability of Success | Payoff from Success | Payoff from Failure | True Expected Value | Estimated Probability of Success (optimistic bias) |
Estimated Expected Value |
|---|---|---|---|---|---|
| 50% | 10 | -10 | 0 | 55% | 1 |
| 50% | 50 | -50 | 0 | 55% | 5 |
| 50% | 100 | -100 | 0 | 55% | 10 |
| 50% | 250 | -250 | 0 | 55% | 25 |
| 50% | 500 | -500 | 0 | 55% | 50 |
Suppose a manager optimistically estimates the probability of success to be 55% (column 5). Column 6 reveals the impact of this optimistic bias. It shows the estimated expected values that arise from the biased probability estimates. The optimistic bias does not affect all projects equally. Riskier projects receive a larger boost in expected value.
Now look at the ranking of the projects by their estimated expected values. The optimistic bias causes the decision-maker to mistakenly reverse the true ranking. The worst choice (bottom row) has the highest estimated expected value and the best choice (top row) has the lowest estimated expected value. Unless risk adjustments (for being risk adverse) fully compensate for the bias, the bias will destroy project selection, causing the decision-maker to forego the best choice and pick the worst one.
This example is especially sensitive to optimism, but it illustrates a fact. Optimistic probabilities give bigger boosts to risky projects. They cause project selection to favor riskier projects, causing project selection errors and unknowningly increasing portfolio risk. The claim that biases, consistently applied, do not impact project selection is wishful thinking that is wrong.
After reading my discussions, many managers wish to share their experiences, thoughts and critiques of my ideas. I always welcome and reply to their comments.
Please share your thoughts with me by using form below. I will send reply to you via email. If you prefer to be contacted by phone, fax or postal mail, please send your comments via my contact page.
© 2014 Pipeline Physics. All rights reserved.