Optimizer's Curse & Portfolio Optimization
An auction house sells a painting. Some
participants overbid, some underbid, but the average of their
bids is correct (unbiased estimates). The "winner" is the
person who overvalues the painting the most.
You buy a house, and enjoying art, you attend auctions. Being a good
judge of artwork, you overvalue art sometimes, undervalue it other
times, but are correct on average. Which auctions do you win? Most
likely, you win when you overvalue artwork.
Eventually, you discover that you overpaid for your paintings.
Exasperated, you exclaim, "I always overvalue artwork!" Your
statement is incorrect. You don't always overvalue artwork; you
overvalue the artwork you buy.
This phenomenon is called the optimizer's curse, and in addition to auctions, it affects portfolio management, creating these problems:
- Consistently overvaluing portfolios, so senior executives suffer reoccurring disappointment as portfolios repeatedly underperform
- Committing many selection errors, funding duds while canceling winners, reducing portfolio value
Unfortunately, the optimizer's curse is counterintuitive, as the following questions illustrate.
Question 1: Using the best information
and best techniques, your best team forecasts blockbuster profit for
a drug in development. Is this forecast the best estimate of the drug's profit?
Question 2: Consider these two statements:
- A forecast is equally likely to be above or below the true value.
- The true value is equally likely to be above or below the forecast.
Suppose statement A is true. Does statement A imply statement B?
The issue here is the forecasting error. All models produce estimates, and all estimates have errors. We might ask, "How do the errors affect decision making? Figures 1-3 illustrate the impact so that we can answer the questions.
Figure 1 presents a probability distribution for the profits of a drug in development, one that highlights the highly skewed distribution of pharmaceutical profits. A reasonable definition of a blockbuster is the 90th percentile of profits, which for this distribution occurs at 1.7.
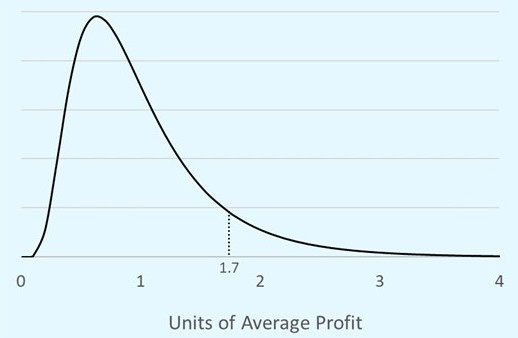
Figure 1: A probability distribution of the profits of a drug in development. The unit of the horizontal axis is the average lifetime profits of a drug (average = total lifetime profits of all drugs / number of drugs).
Figure 2 shows a large but reasonable error for forecasting the value of drugs in development. The forecasting error is symmetrical, a normal distribution, so the errors are unbiased.
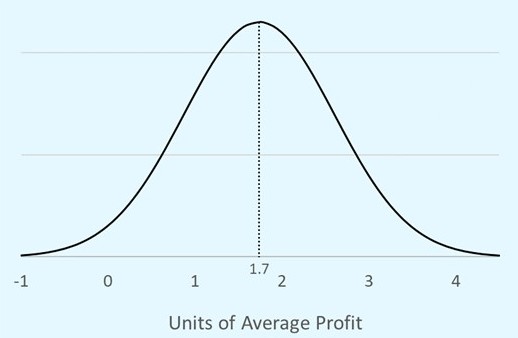
Figure 1: A probability distribution of the forecast for a drug that has a true value of 1.7. The forecasts is unbiased and equally likely to be above or below the true value s(Statement A, above).
Figure 3 shows the probability distribution of profit, given a forecast of 1.7. Notice two qualities. Even though the error is unbiased (statement A and Figure 2, above), a forecast of blockbuster profit is, on average, highly biased, in this example, 42% too high. Moreover, the chance of the true value equaling or exceeding the forecast is only 14%.
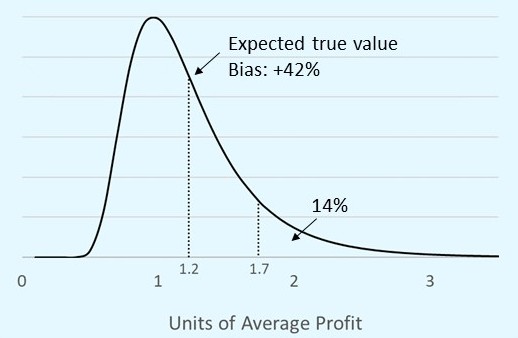
Figure 3: The probability distribution of the true value of a drug that is forecast to be a blockbuster.
We can now answer questions 1 and 2:
Question 1: If the best information, best technique, and
best forecasting team estimate blockbuster profits, their estimate is
likely to be optimistic. In this realistic example, reducing the
estimate by 42% produces the best forecast.
Question 2: For a forecast of blockbuster profits, the true value is more
likely to be below than above the forecast. In this realistic example,
the true value has an 86% chance of being below the forecast.
Labeling a model's output as defensible or treating the output of a model as "our version of the truth," is an error. Why? These declarations erroneously treat an estimate as if it were the true value. They ignore the impact of estimation errors.
Notice the following asymmetry. From the point of view of the true value (Figure 2), the forecasts are unbiased. From the point of view of the forecasts (Figure 3), which is all we know, biases exist. How do biased forecasts arise from unbiased errors? Here are three explanations.
- A company has few opportunities to correctly forecasts the profits of blockbusters but many opportunities to overestimate the value of average compounds. Thus, many forecasts for blockbuster profits are false-positives.
- Large, positive forecasting errors produce high forecasts, so forecasting errors induce a positive correlation between forecasts and errors. On average, high forecasts are optimistic.
- For the mathematically inclined: Figure 2 presents the possible forecasts given a true value. Figure 3 presents the possible true values given a forecast. The figures "flip" a conditional probability, which requires Bayes' law. Propagating Figure 1's and Figure 2's probability distributions through Bayes' law produces Figure 3.
How do the biases affect project selection? Whether creating portfolios via executive discussions, cutoff values, rankings, optimization, or simulation optimization, the following expectations always occur:
- Overvalued portfolios
- Project selection errors that reduce portfolio value
- Senior executives suffer reoccurring disappointment, as portfolios persistently underperform.
In sum, portfolio management suffers the optimizer's curse.
For additional information about the optimizer's curse, plus methods for mitigating it, please read our papers:
- In Pharmaceutical Executive magazine: Product Development: The Optimizer's Curse
- White paper: How to Remove Chronic Optimism from your Compound and Portfolio Evaluations while Creating More Value
- Academic article: Friction and Decision Rules in Portfolio Decision Analysis
If you wish, kindly share your thoughts by using the form below, via phone (503.332.4095) or LinkedIn. Your concerns, thoughts, and ideas are the most important ones.